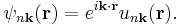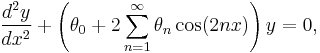Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle (usually, an electron) placed in a periodic potential. Bloch's theorem states that the energy eigenfunction for such a system may be written as the product of a plane wave envelope function and a periodic function (periodic Bloch function) 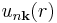 that has the same periodicity as the potential:
that has the same periodicity as the potential:
The corresponding energy eigenvalues are ϵn(k) = ϵn(k + K), periodic with periodicity K of a reciprocal lattice vector. The energies associated with the index n vary continuously with wave vector k and form an energy band identified by band index n. The eigenvalues for given n are periodic in k; all distinct values of ϵn(k) occur for k-values within the first Brillouin zone of the reciprocal lattice.
In fact, the Bloch theorem is a direct consequence of the translational symmetry of crystals, which means that the crystal is invariant under a translational movement  of the form
of the form 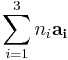 , where
, where 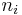 are integers and
are integers and 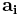 are the primitive lattice vectors. If
are the primitive lattice vectors. If 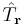 denotes the translation operation that can be applied to a wave function in a direction of the form
denotes the translation operation that can be applied to a wave function in a direction of the form 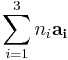 , where
, where 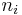 are integers, it can readily be seen that the operation forms a group with the same combination law as
are integers, it can readily be seen that the operation forms a group with the same combination law as 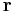 . Since the crystalline system and hence its Hamiltonian is invariant after such translations, the translation operator must be commutative with the Hamiltonian operator, thus they can be simultaneously diagonalized. In this way, each eigenfunction of the Hamiltonian can be an eigenfunction of the translation operator. To maintain the wavefunction properly normalized, the eigenvalue for the translation operator must be of the form
. Since the crystalline system and hence its Hamiltonian is invariant after such translations, the translation operator must be commutative with the Hamiltonian operator, thus they can be simultaneously diagonalized. In this way, each eigenfunction of the Hamiltonian can be an eigenfunction of the translation operator. To maintain the wavefunction properly normalized, the eigenvalue for the translation operator must be of the form 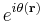 , where
, where 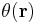 is a function of the translation vector
is a function of the translation vector 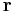 . By applying two such translations
. By applying two such translations 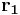 and
and 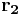 consecutively to one wavefunction, it can be shown that
consecutively to one wavefunction, it can be shown that 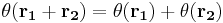 . Thus the
. Thus the 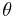 function can be written as the dot product of the translation vectors
function can be written as the dot product of the translation vectors 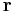 and a vector
and a vector 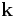 because of the linearity of
because of the linearity of 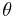 . In this way, it has been deduced that an eigenfunction of the Hamiltonian operator of a system with discrete translational symmetry such as a crystal is always an eigenfunction of the discrete symmetrical translation operators
. In this way, it has been deduced that an eigenfunction of the Hamiltonian operator of a system with discrete translational symmetry such as a crystal is always an eigenfunction of the discrete symmetrical translation operators 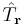 with eigenvalue
with eigenvalue 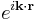 . In other words, each eigenvalue of the Hamiltonian forms a basis for a one-dimensional representation of the group of translation operations specified by the Bravais lattice and the vector
. In other words, each eigenvalue of the Hamiltonian forms a basis for a one-dimensional representation of the group of translation operations specified by the Bravais lattice and the vector 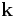 can be considered to be a label for the irreducible representation.
can be considered to be a label for the irreducible representation.
More generally, a Bloch-wave description applies to any wave-like phenomenon in a periodic medium. For example, a periodic dielectric in electromagnetism leads to photonic crystals, and a periodic acoustic medium leads to phononic crystals. It is generally treated in the various forms of the dynamical theory of diffraction.
The plane wave vector (Bloch wave vector) k, which when multiplied by the reduced Plank's constant is the particle's crystal momentum, is unique only up to a reciprocal lattice vector, so one only needs to consider the wave vectors inside the first Brillouin zone. For a given wave vector and potential, there are a number of solutions, indexed by n, to Schrodinger's equation for a Bloch electron. These solutions, called bands, are separated in energy by a finite spacing at each k; if there is a separation that extends over all wave vectors, it is called a (complete) band gap. The band structure is the collection of energy eigenstates within the first Brillouin zone. All the properties of electrons in a periodic potential can be calculated from this band structure and the associated wave functions, at least within the independent electron approximation.
A corollary of this result is that the Bloch wave vector k is a conserved quantity in a crystalline system (modulo addition of reciprocal lattice vectors), and hence the group velocity of the wave is conserved. This means that electrons can propagate without scattering through a crystalline material, almost like free particles, and that electrical resistance in a crystalline conductor only results from imperfections and finite size which break the periodicity and induce interaction with phonons.
The concept of the Bloch state was developed by Felix Bloch in 1928, to describe the conduction of electrons in crystalline solids. The same underlying mathematics, however, was also discovered independently several times: by George William Hill (1877), Gaston Floquet (1883), and Alexander Lyapunov (1892). As a result, a variety of nomenclatures are common: applied to ordinary differential equations, it is called Floquet theory (or occasionally the Lyapunov–Floquet theorem). Various one-dimensional periodic potential equations have special names, for example, Hill's equation:[1]
where the 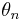 are constants. Hill's equation is very general, as the θ-related terms may be viewed as a Fourier series expansion of a periodic potential. Other much studied periodic one-dimensional equations are the Kronig–Penney model and Mathieu's equation.
are constants. Hill's equation is very general, as the θ-related terms may be viewed as a Fourier series expansion of a periodic potential. Other much studied periodic one-dimensional equations are the Kronig–Penney model and Mathieu's equation.
Graphical representation of Bloch Function
References
- ^ Magnus, W; Winkler, S (2004). Hill's Equation. Courier Dover. p. 11. ISBN 0-0486495655. http://books.google.com/?id=ML5wm-T4RVQC&dq=%22hill's+equation%22&printsec=frontcover#PPA11,M1.
See also
- Electronic band structure
- Tight-binding model
- Nearly-free electron model
- Wannier function
- Bloch oscillations
- Bloch wave – MoM method
Further reading
- Kittel, Charles (1996). Introduction to Solid State Physics. New York: Wiley. ISBN 0471142867.
- Neil W. Ashcroft and N. David Mermin (1976). Solid State Physics. Orlando: Harcourt. ISBN 0030493463.
- Felix Bloch (1928). "Über die Quantenmechanik der Elektronen in Kristallgittern". Z. Physik 52: 555–600. Bibcode 1929ZPhy...52..555B. doi:10.1007/BF01339455.
- George William Hill (1886). "On the part of the motion of the lunar perigee which is a function of the mean motions of the sun and moon". Acta Math. 8: 1–36. doi:10.1007/BF02417081. This work was initially published and distributed privately in 1877.
- Gaston Floquet (1883). "Sur les équations différentielles linéaires à coefficients périodiques". Ann. École Norm. Sup. 12: 47–88.
- Alexander Mihailovich Lyapunov (1992). The General Problem of the Stability of Motion. London: Taylor and Francis. Translated by A. T. Fuller from Edouard Davaux's French translation (1907) of the original Russian dissertation (1892).
- H. Föll. "Periodic Potentials and Bloch's Theorem – lectures in "Semiconductors I"". The University of Kiel. http://www.tf.uni-kiel.de/matwis/amat/semi_en/kap_2/backbone/r2_1_4.html.
- M.S.P. Eastham (1973). The Spectral Theory of Periodic Differential Equations. Texts in Mathematics. Edinburgh: Scottish Academic Press.